Все электронные компоненты выделяют тепло, поэтому умение рассчитывать радиаторы так, чтобы не пролетать в прикидках на пару порядков очень полезно любому электронщику.

Тепловые расчеты очень просты и имеют очень много общего с расчетами электронных схем. Вот, посмотрите на обычную задачу теплового расчета, с которой я только что столкнулся

Задача

Нужно выбрать радиатор для 5-вольтового линейного стабилизатора, который питается от 12вольт максимум и выдает 0.5А. Максимальная выделяемая мощность получается (12-5)*0.5 = 3.5Вт

Погружение в теорию

Для того, чтобы не плодить сущностей, люди почесали тыковку и поняли, что тепло очень похоже на электрической ток, и для тепловых расчетов можно использовать обычный закон Ома, только

1. Напряжение (U) заменяется  температурой (T)
2. Ток (I) заменяется мощностью (P)
3. Сопротивление заменяется тепловым сопротивлением. Обычное сопротивление имеет размерность Вольт/Ампер, а тепловое – °C/Ватт

В итоге, закон Ома заменяется на свой тепловой аналог:

Небольшой замечание – для того, чтобы обозначить, что имеется ввиду тепловое (а не электрическое) сопротивление, к букве R,  дописывают букву тэта:на клавиатуре у меня такой буквы нет, а копировать из таблицы символов лень, поэтому я буду пользоваться просто буквой R.

Продолжаем

Тепло выделяется в кристалле стабилизатора, а наша цель – не допустить его перегрева (не допустить перегрева именно кристалла, а не корпуса, это важно!).

До какой температуры можно нагревать кристалл, написано в даташите:

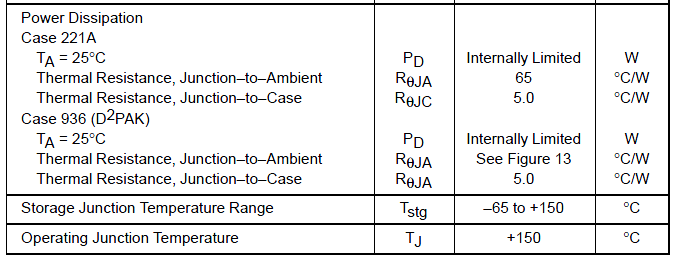
Обычно, предельную температуру кристалла называют Tj (j = junction = переход – термочувствительные внутренности микросхем в основном состоят из pn переходов. Можно считать, что температура переходов равна температуре кристалла)

Без радиатора

Попробуем рассчитать, до какой температуры нагреется кристалл, если не ставить радиатор.

Тепловая схема выглядит очень просто: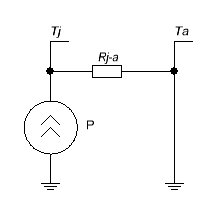

Специально для случаев использования корпуса без радиатора, в даташитах пишут тепловое сопротивление кристалл-атмосфера (Rj-a) (что такое j вы уже в курсе, a = ambient = окружающая среда)

Заметьте, что температура “земли” не нулевая, а равняется температуре окружающего воздуха (Ta). Температура воздуха зависит от того, в каких условиях находится радиатор Если стоит на открытом воздухе, то можно положить Ta = 40 °C, а вот, если в закрытой коробке, то температура может быть значительно выше!

Записываем тепловой закон Ома: Tj = P*Rj-a + Ta. Подставляем P = 3.5, Rj-a = 65, получаем Tj = 227.5 + 40 = 267.5 °C. Многовато, однако!

Цепляем радиатор

Тепловая схема нашего примера со стабилизатором на радиаторе становится вот такой:

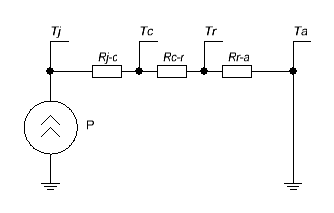
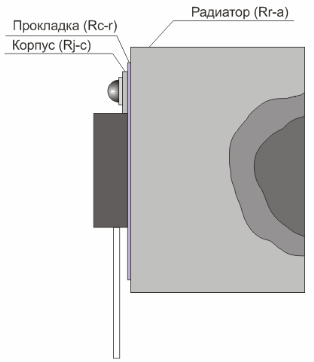
• Rj-c – сопротивление от кристалла до теплоотвода корпуса (c = case = корпус ). Дается в даташите. В нашем случае – 5 °C/Вт – из даташита
• Rc-r – сопротивление корпус-радиатор. Тут не все так просто. Это сопротивление зависит от того, что находится между корпусом и радиатором. К примеру, силиконовая прокладка имеет коэффициент теплопроводности 1-2 Вт/(м*°C), а паста КПТ-8 – 0.75Вт/(м*°C). Тепловое сопротивление можно получить из коэффициента теплопроводности по формуле:

  R = толщина прокладки/(коэффициент теплопроводности * площадь одной стороны прокладки)

  Часто Rc-r вообще можно игнорировать. К примеру, в нашем случае (используем корпус TO220, с пастой КПТ-8, средняя глубина пасты, взятая с потолка – 0.05мм). Итого, Rc-r = 0.5 °C/Вт. При мощности 3.5вт, разница температур корпуса стабилизатора и радиатора — 1.75градуса. Это – не много. Для нашего примера, возьмем Rc-r = 2 °C/Вт

• Rr-a – тепловое сопротивление между радиатором и атмосферой. Определяется геометрией радиатора, наличием обдува, и кучей других факторов. Этот параметр намного проще измерить, чем посчитать (см в конце статьи). Для примера — Rr-c = 12.5 °C/Вт
• Ta = 40°C – тут мы прикинули, что атмосферная температура редко выше, можно взять и 50 градусов, чтобы уж точно было.

Подставляем все эти данные в закон Ома, и получаем Tj = 3.5*(5+2+12.5) + 40 = 108.25 °C

Это значительно меньше, чем предельные 150 °C. Такой радиатор можно использовать. При этом, корпус радиатора будет греться до Tc = 3.5*12.5 + 40 = 83.75 °C. Такая температура уже способна размягчить некоторые пластики, поэтому нужно быть осторожным.

Измерение сопротивления радиатор-атмосфера.

Скорее-всего, у вас уже валяется куча радиаторов, которые можно задействовать. Тепловое сопротивление измеряется очень легко. Это этого нужно сопротивление и источник питания.

Лепим сопротивление на радиатор, используя термопасту:

Подключаем источник питания, и выставляем напряжение так, чтобы на сопротивлении выделялась некая мощность. Лучше, конечно, нагревать радиатор той мощностью, которую он будет рассеивать в конечном устройстве (и в том положении, в котором он будет находиться, это важно!). Я обычно оставляю такую конструкцию на пол часа, чтобы она хорошо прогрелась.

После того, как измерили температуру, можно рассчитать тепловое сопротивление

Rr-a = (T-Ta)/P. К примеру, у меня радиатор нагрелся до 81 градуса, а температура воздуха – 31 градус. таким образом, Rr-a = 50/4 = 12.5 °C/Вт.

Прикидка площади радиатора

В древнем справочнике радиолюбителя приводился график, по которому можно прикинуть площадь радиатора. Вот он:

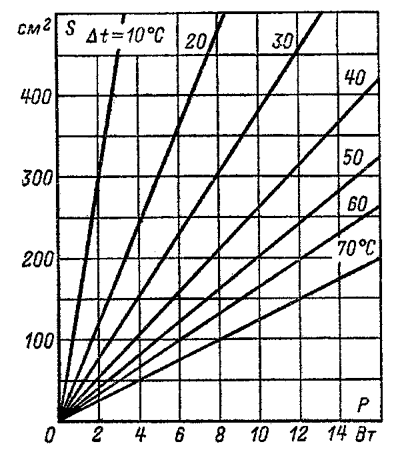
Работать с ним очень просто. Выбираем перегрев, который хочется получить и смотрим, какая площадь соответствует необходимой мощности при таком перегреве.

К примеру, при мощности 4вт и перегреве 20 градусов, понадобится 250см^2 радиатора. Этот график дает завышенную оценку площади, и не учитывает кучу факторов как то принудительный обдув, геометрия ребер, итп.